Fast Fourier Transformation (FFT) with OXYGEN

Fast Fourier Transformation (FFT) – How it began
Since the beginning of time, periodic processes play an important role, whether in nature or technology. These include, for example, planet movements or the pulse beat. Joseph Fourier (1768-1830) defined the basic principle for their analysis in the Fourier Theorem.
The Fourier theorem lays the foundation of the Fast Fourier Transformation (FFT). It states that every signal waveform in the time domain can be represented by the weighted sum of the sine and cosine oscillations. The series expansion of a periodic, sectionally continuous function into a function series of sine and cosine functions is called Fourier series.
With the help of the Fourier Transformation it is thus possible to transform signals from the time domain into a frequency domain. Therefore, the representation changes from time and sample values to frequency components, amplitude and/or phase. This is important as many operations are easier to perform in frequency domains (e.g. filters).
From Discrete Fourier Transformation (DFT) to Fast Fourier Transformation (FFT)
The considerations above first led to the Discrete Fourier Transformation (DFT). It is an algorithm to determine spectral components of periodic, discrete signals. Thereby, it provides information about the composition of a signal & thus allows studying the individual components in the frequency domain. With the help of DFT, we can analyze digital signals – which is not possible with continuous signals. However, the algorithm of DFT involves a high calculation effort. The processing time of an algorithm strongly depends on the number of needed multiplications. Therefore, it takes long to calculate the N spectral values of the DFT since N^2 multiplications are needed.
This is how the Fast Fourier Transformation (FFT) was born. Opposing the direct calculation, the Fast Fourier Transformation (FFT) reuses previously calculated intermediate results. Due to that, you need fewer multiplications and less time. The best known method originates from James Cooley and John W. Tukey (1965).
An example to illustrate the difference
The comparison of the two algorithms reveals why the Fast Fourier Transformation (FFT) is so popular. In our example we assume a block length of N=1024. While a computer needs to calculate about 1,000,000 multiplications for the DFT, the FFT only requires about 10,000 – i.e. only one hundredth.
Fast Fourier Transformation (FFT) applied with OXYGEN
DEWETRON developed a comprehensive & intuitive FFT feature exclusively for OXYGEN users. It supports every application with the highest flexibility and easiest handling. In the following list, you can find aspects that distinguish OXYGEN’s FFT feature:
- Freely selectable (not only 2^N) number of input samples or line resolution
- Optional zero-padding for higher line resolution
- 7 different window types
- Spectrum analyzer instrument with 18 different scaling types (amplitude, RMS, PSD, decibel, …)
- Average and overlap feature
- Spectrogram instrument for time-dependent analysis with selectable color map
- FFT reference curves feature shows two reference curves in the spectrum analyzer. It changes the instruments’ background color in case the threshold is exceeded. You can define values via a table from any program (e.g. Excel). Afterwards, you can simply copy and paste them.
In figure 1, you can see an example of an FFT in OXYGEN:
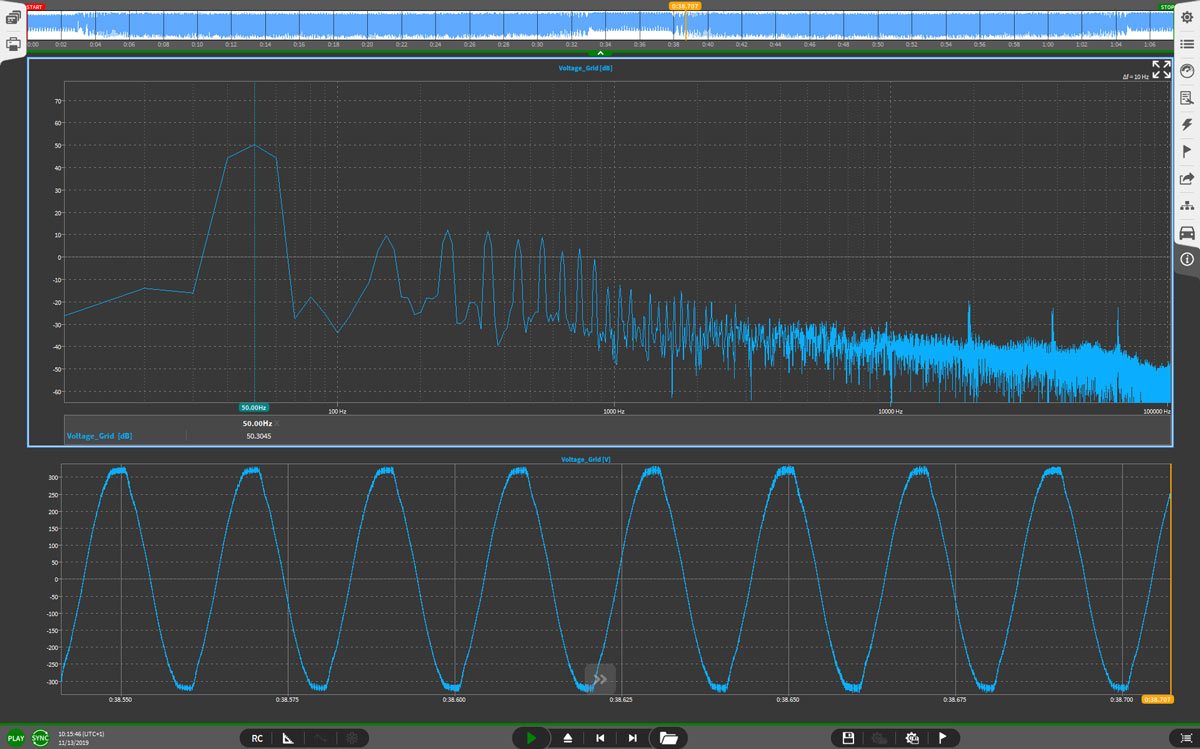
Figure 1
Foundation & Theory
Some recognized institutions provide valuable contributions to the Fourier series, Fourier Transformation, DFT, FFT. Here, you can find a collection of useful links:
Who is DEWETRON?
DEWETRON is responsible for the development of OXYGEN – the most intuitive measurement software, you will probably ever see. Apart from high-end software, DEWETRON offers a variety of high-precision measurement systems to customers from different fields. Thus, DEWETRON helps to make the world more predictable and safer. Follow us on LinkedIn and YouTube to never miss any updates.

Questions, thoughts, feedback? Simply send us a message. We are looking forward to reading from you.





