Fast Fourier Transformation (FFT) mit OXYGEN

Fast Fourier Transformation (FFT) – Wie alles begann
Schon seit Anbeginn der Zeit spielen periodische Vorgänge eine wichtige Rolle, egal ob in der Natur oder in der Technik. Zu diesen periodischen Vorgängen gehören beispielsweise die Planetenbewegung oder auch der Pulsschlag. Das Grundprinzip für die Analyse solcher Vorgänge, hat bereits Jean Baptiste Joseph Fourier (1768-1830) im Fourier-Theorem definiert.
Das Fourier-Theorem ist die Basis der Fast Fourier Transformation (FFT). Es sagt aus, dass jeder Signalverlauf im Zeitbereich durch die gewichtete Summe der Sinus- und Cosinus-Schwingungen dargestellt werden kann. Die Reihenentwicklung einer periodischen, abschnittsweise stetigen Funktion in eine Funktionenreihe aus Sinus- und Cosinus-Funktionen nennt man Fourier Reihe.
Mithilfe der Fourier Transformation ist es so möglich, Signale vom Zeitbereich in einen Frequenzbereich zu transformieren. Das heißt also, dass sich die Darstellung mit Zeitpunkt und Abtastwert zu einer Darstellung mit Frequenzanteil, Amplitude und/oder Phase ändert. Das ist deswegen wichtig, weil viele Operationen wie z.B. Filter im Frequenzraum wesentlich leichter durchführbar sind.
Von der Diskreten Fourier Transformation (DFT) zur Fast Fourier Transformation (FFT)
Aus den obenstehenden Überlegungen entwickelte sich zuerst die diskrete Fourier Transformation (DFT). Sie ist eine Rechenvorgabe, um Spektralkomponenten von periodischen, diskreten Signalen zu bestimmen. So bringt sie Aufschluss über die Zusammensetzung eines Signals und erlaubt damit die Sicht auf die einzelnen Komponenten im Frequenzbereich. Mithilfe der DFT ist es uns also möglich, digitale Signale zu verarbeiten und zu analysieren – etwas, das bei kontinuierlichen Signalen so nicht möglich ist. Der Algorithmus der DFT bringt allerdings einen sehr hohen Aufwand mit sich. Die Verarbeitungszeit eines Algorithmus hängt stark von der Anzahl der Multiplikationen ab, die der Rechner ausführen muss. So werden für die Berechnung der N Spektralwerte der DFT N^2 komplexe Multiplikationen benötigt.
Und deswegen entstand sie – die schnellere Berechnung der DFT – die Fast Fourier Transformation (FFT). Anders als bei der direkten Berechnung werden bei der Fast Fourier Transformation (FFT) zuvor berechnete Zwischenergebnisse wiederverwendet. So können arithmetische Rechenoperationen eingespart und der Zeitaufwand verkürzt werden. Das bekannteste Verfahren dafür haben James Cooley und John W. Tukey 1965 veröffentlicht.
Ein Beispiel zum Vergleich
Der Vergleich der beiden mathematischen Verfahren gibt Aufschluss darüber, warum sich die Fast Fourier Transformation (FFT) an so großer Beliebtheit erfreut. In unserem Beispiel nehmen wir eine Blocklänge von N=1024 an. Während bei der DFT dafür ca. 1,000,000 Multiplikationen berechnet werden müssen, sind es bei der FFT nur ca. 10,000 – also nur ein Hundertstel.
Fast Fourier Transformation (FFT) in der Praxis
DEWETRON hat exklusiv für die Nutzer und Nutzerinnen der Messsoftware OXYGEN ein umfangreiches und intuitives FFT-Instrument entwickelt. Damit unterstützt OXYGEN jede Applikation mit höchster Flexibilität und einfachster Bedienung. In der folgenden Liste finden Sie einige Aspekte, die das FFT-Instrument unserer OXYGEN ausmachen:
- Frei auswählbare (nicht nur 2^N) Anzahl von Eingangssamples oder Linienauflösung
- Optionales Zero-Padding für eine höhere Linienauflösung
- 7 verschiedene Fenstertypen
- FFT-Instrument mit 18 verschiedenen Skalierungstypen (Amplitude, RMS, PSD, Dezibel, …)
- Mittelung und Überlappung
- Spektrogramm-Instrument für eine zeitabhängige Analyse mit auswählbaren Farbtabellen
- Die Funktion FFT-Referenzkurven (verfügbar ab OXYGEN 5.3) zeigt zwei Referenzkurven im FFT Instrument an. Wenn der Schwellenwert überschritten wird, ändert sich die Hintergrundfarbe. Die Werte können über eine Tabelle aus anderen Programmen wie z.B. Excel definiert werden. So können Sie diese einfach kopieren und einfügen.
In folgender Abbildung 1 sehen Sie ein Beispiel einer FFT in OXYGEN:
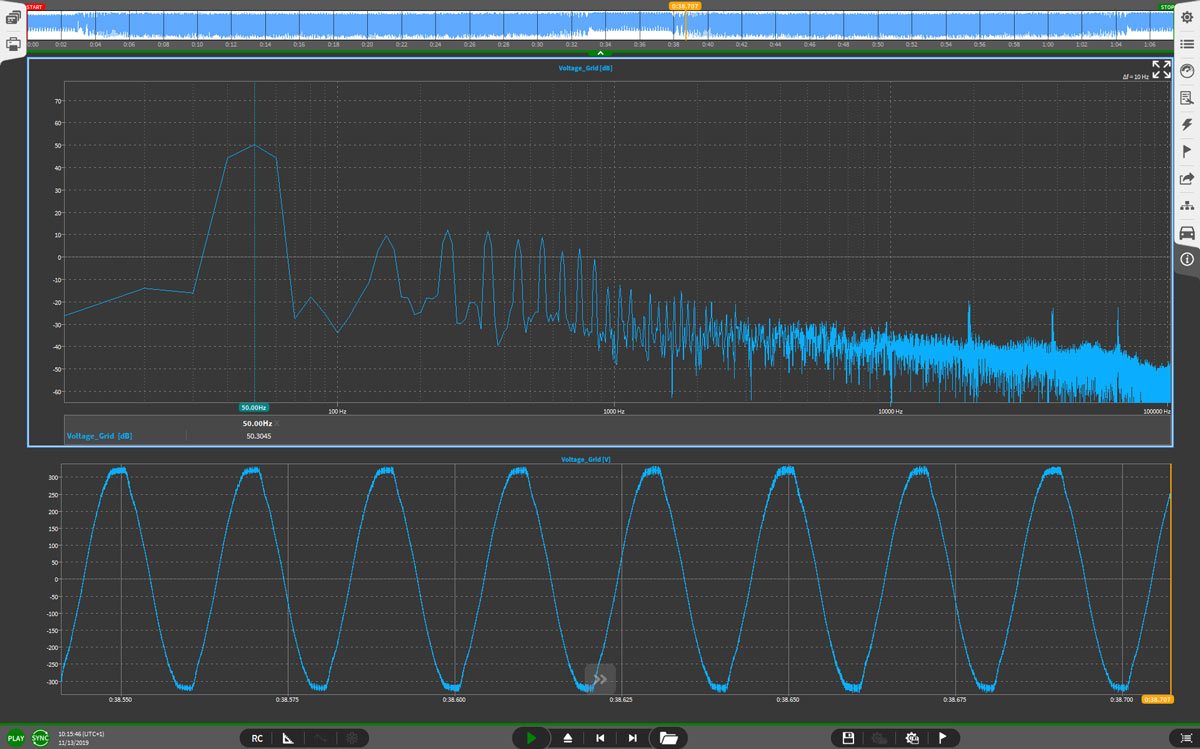
Abbildung 1
Grundlagen & Theorie
Einige anerkannte Institutionen haben wertvolle Beiträge zur Fourier Reihe, Fourier Transformation, DFT, FFT geleistet. Hier finden Sie eine Sammlung nützlicher Links:
Wer ist DEWETRON?
DEWETRON steht hinter der Entwicklung von OXYGEN – der intuitivsten Messsoftware, die Sie vermutlich jemals sehen werden. Abgesehen davon bietet DEWETRON Kundinnen und Kunden aus den unterschiedlichsten Bereichen eine Vielfalt hochpräziser Messsysteme an. So hilft DEWETRON, die Welt berechenbarer und sicherer zu machen. Folgen Sie uns auf LinkedIn und YouTube, um keine Updates zu verpassen.

Fragen, Anregungen, Feedback? Schreiben Sie uns hier. Wir freuen uns auf den Austausch!





