Die DQ-Analyse für Drehfeldmaschinen || Whitepaper

Einleitung
Die DQ-Analyse, gleichbedeutend mit der Park-Transformation, wird dafür verwendet, die auftretenden Wechselgrößen in Drehfeldmaschinen, wie elektrische Ströme, induzierte Spannungen oder verkettete Flüsse in Gleichgrößen zu überführen.
Dies bietet Vorteile für die Analyse und Regelung elektrischer Maschinen. Namensgebend für die DQ-Analyse sind die direkte Achse (d-Achse) und die Quadratur Achse (q-Achse) des zugehörigen Koordinatensystems (KOS).
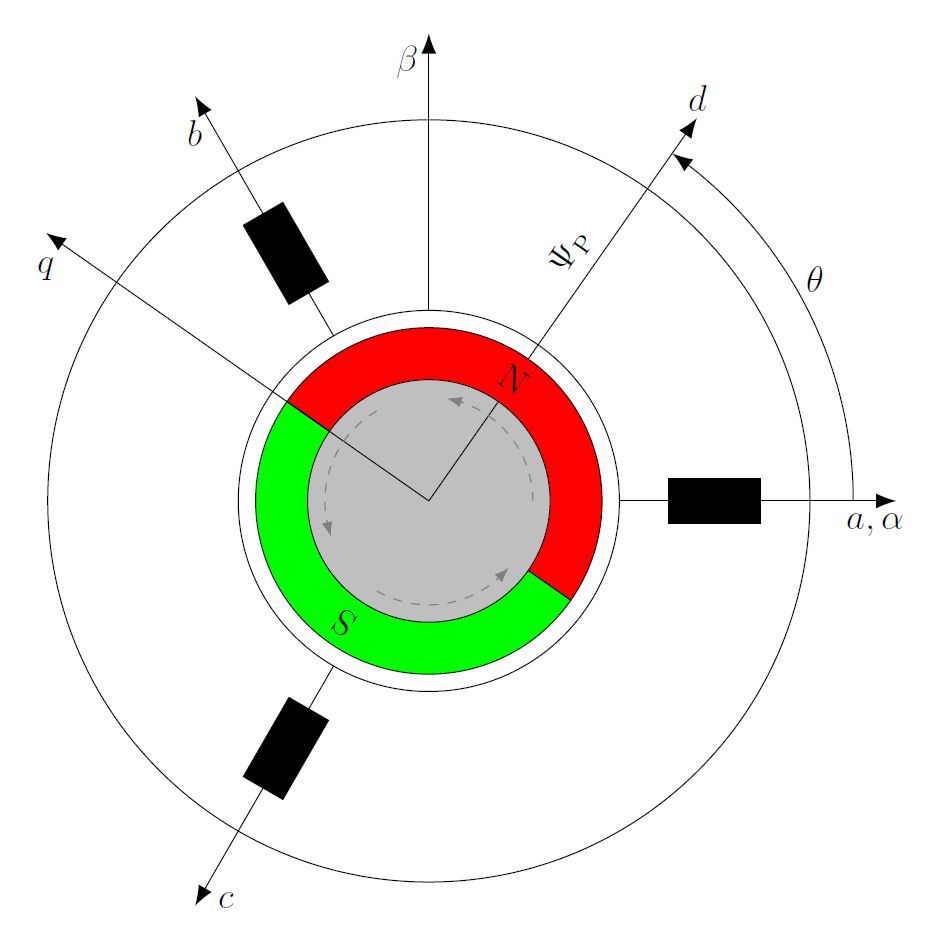
Abb. 1: Koordinatensysteme einer 2-poligen Synchronmaschine
In obiger Abbildung sind die für Drehfeldmaschinen relevanten Koordinatensysteme im vereinfachten Querschnitt einer Synchronmaschine gezeigt. Folgende Achsen sind dargestellt:
- a-, b- und c-Achse des abc- bzw. uvw-Koordinatensystems
- α– und β-Achse des αβ-Koordinatensystems
- d- und q-Achse des dq-Koordinatensystems
Auch der verkettete Fluss des Rotors, der sogenannte Polradfluss ΨP und der Rotorwinkel θ sind erkennbar. Grundlegende Idee der DQ-Analyse ist das dreiphasige System einer Drehfeldmaschinen mit jeweils um 120° versetzten Achsen auf orthogonale, also rechtwinklige Systeme, mit um 90° versetzten Achsen, abzubilden. Mit der Clarke-Transformation erhält man das am Stator fixierte αβ-KOS. Lässt man dieses Koordinatensystem synchron mit dem Rotor mitrotieren, erhält man über die Park-Transformation das rotor- bzw. drehfeldfeste dq-KOS. Bevor auf die mathematische Beschreibung dieser Transformationen eingegangen wird, werden diese auf anschauliche Weise in folgenden Diagrammen dargestellt.
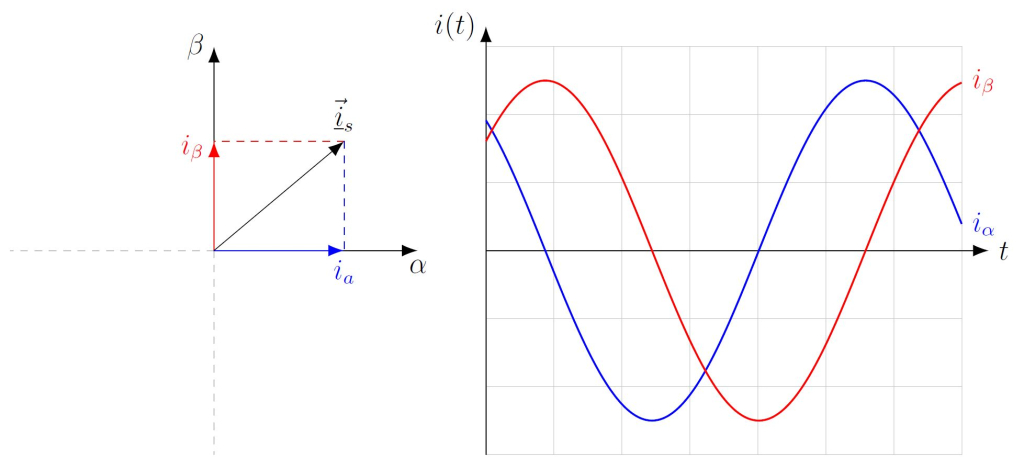
Abb. 2: Das uvw- bzw. abc-Koordinatensystem
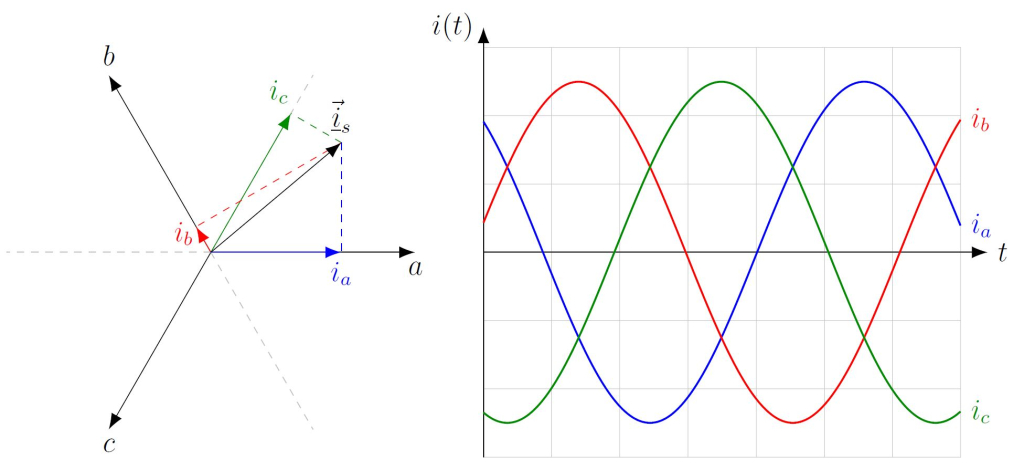
Abb. 3: Das αβ-Koordinatensystem
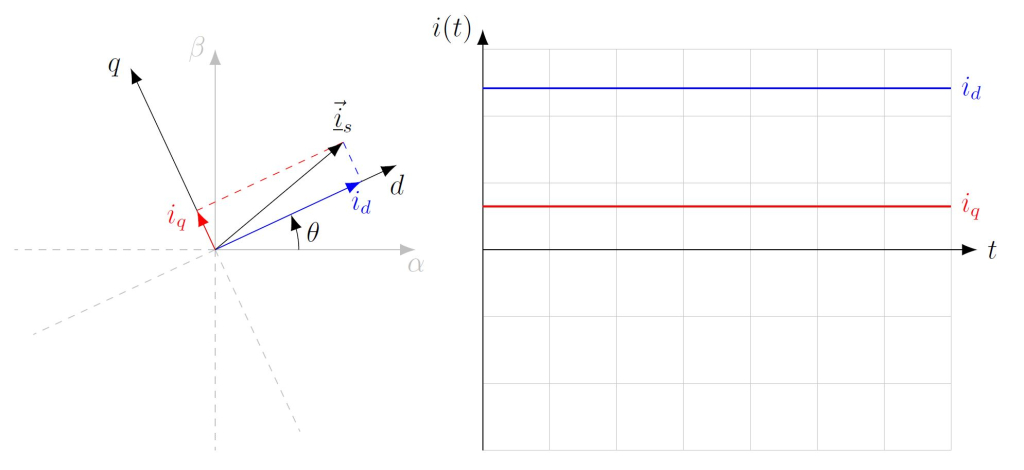
Abb. 4: Das dq-Koordinatensystem
Die Aufspaltung des am Magnetfeld des Rotors orientierten Koordinatensystems in eine d- und q-Achse ermöglicht bei der feldorientierten Regelung eine separate Stellung der drehmomentbildenden Größe iq und der feldbildenden Größe id . Ein von den Wicklungen des Stators erzeugtes Magnetfeld entlang der d-Achse verstärkt oder schwächt das von den Permanentmagneten des Rotors entwickelte Magnetfeld und bewirkt kein Drehmoment. Dies wird in der sogenannten Feldschwächung ausgenutzt, um Drehzahlen zu erreichen, die den Grunddrehzahlbereich der Maschine übersteigen. Ein positiver Strom iq erzeugt einen positiven magnetischen Fluss entlang der q-Achse und somit ein Drehmoment in positive Drehrichtung. Ein negativer Strom iq erzeugt ein Drehmoment in negative Drehrichtung, also im Uhrzeigersinn.
CLARKE-TRANSFORMATION
Die Clarke-Transformation bildet die um 120° versetzten Stranggrößen der Maschine im uvw- bzw. abc-KOS auf zwei um 90° versetzte Größen in das αβ-KOS ab. Diese Umformung wird auch als 3→2−Transformation bezeichnet. Die amplitudeninvariante Clarke-Transformation unter Voraussetzung eines symmetrischen Dreiphasensystems lässt sich wie folgt darstellen:
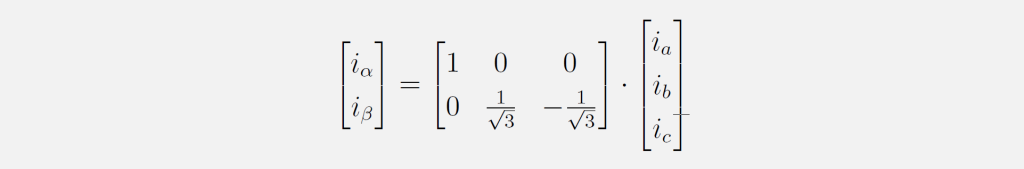
Diese Umrechnung ist mit der inversen Clarke-Transformation reversibel:
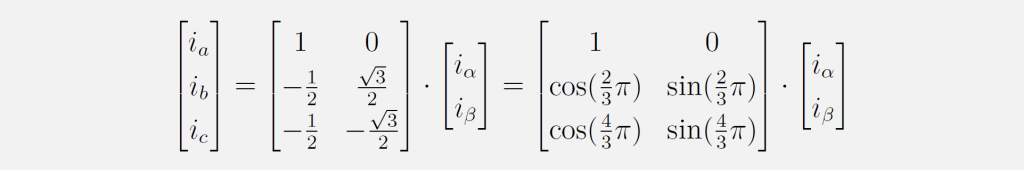
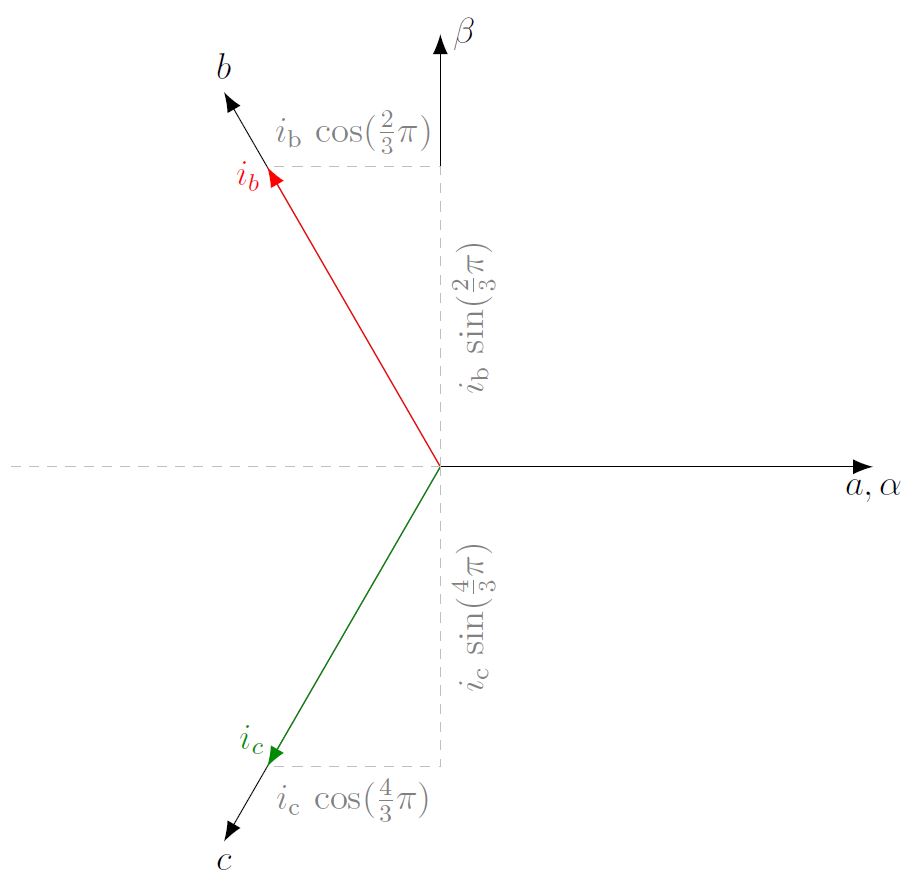
Abb. 5: Visualisierung der Clarke-Transformation
Nach der Clarke-Transformation sind die drei Größen des symmetrischen Dreiphasensystems auf zwei Wechselgrößen im statorfesten αβ-KOS abgebildet. Rotiert man nun dieses Koordinatensystem um den elektrischen Rotorwinkel θ, erhält man mit der Park-Transformation das rotor- bzw. drehfeldfeste dq-KOS:
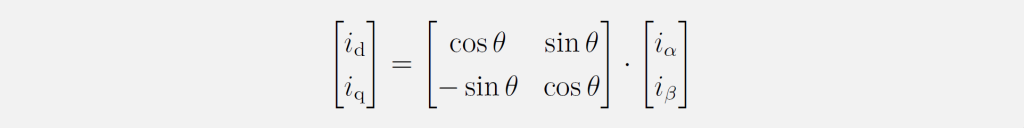
Diese Operation ist mit der inversen Park-Transformation reversibel:
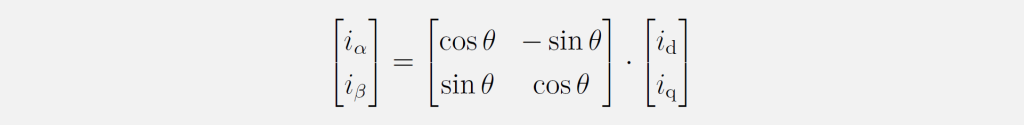
Das dq-KOS rotiert bei der Synchronmaschine gekoppelt am Rotor mit der gleichen elektrischen Frequenz wie das Drehfeld. Dadurch ergeben sich im stationären Betrieb Gleichgrößen für die Ströme id und iq . Die Park-Transformation ist mit der verwendeten Trigonometrie in folgendem Diagramm anschaulich dargestellt.
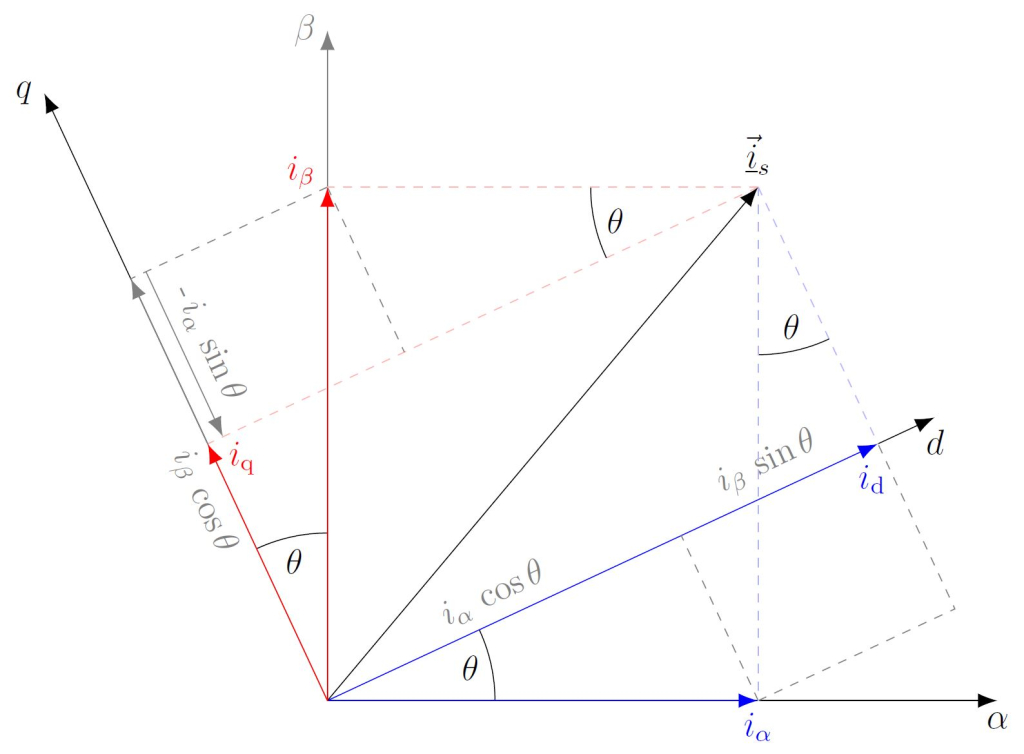
Abb. 6: Visualisierung der Park-Transformation
Dieses Koordinatensystem besitzt eine direkte bzw. d-Achse und eine Quadraturbzw. q-Achse, die 90° vor der d-Achse orientiert ist. Die d-Achse zeigt in die gleiche Richtung wie der Zeiger des Polradflusses ΨP.
Bei der Park-Transformation wird [iα iβ]T über eine Rotationsmatrix gedreht. Es bietet sich an, die αβ → dq und dq → αβ Umrechnungen mit den komplexen Zeigern iαβ = iα + j · iβ und idq = id + j · iq in verkürzter komplexer Darstellung zu formulieren:
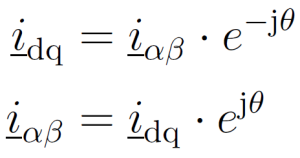
Sind iα, iβ und id, iq bekannt, lässt sich daraus der elektrische Rotorwinkel extrahieren.
Die Park-Transformation und auch die inverse Park-Transformation lassen sich im symmetrischen Dreiphasensystem allgemein auch ohne den Zwischenschritt über die Clarke-Transformation definieren:
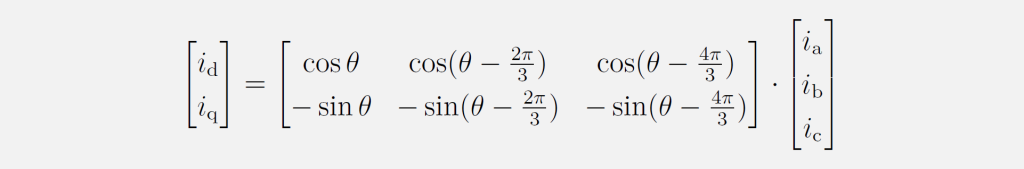
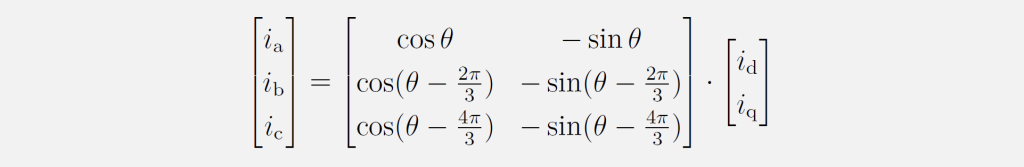
Alle beschriebenen Koordinatensystemtransformationen stellen die Größen des Dreiphasensystems nur auf andere Weise dar. Bei den Transformationen gehen keine Informationen verloren. Deswegen kann man ohne Weiteres die Transformation mit der zugehörigen inversen Variante umkehren. Analog können diese Umwandlungen auch auf Spannungen und magnetische Flüsse angewendet werden.
Im stationären Betrieb, also bei konstantem Drehmoment und konstanter Drehzahl, ergeben sich für die Spannungs- und Stromverläufe im dq-KOS Gleichgrößen, die eine Struktur analog zur Regelung einer Gleichstrommaschine ermöglichen.
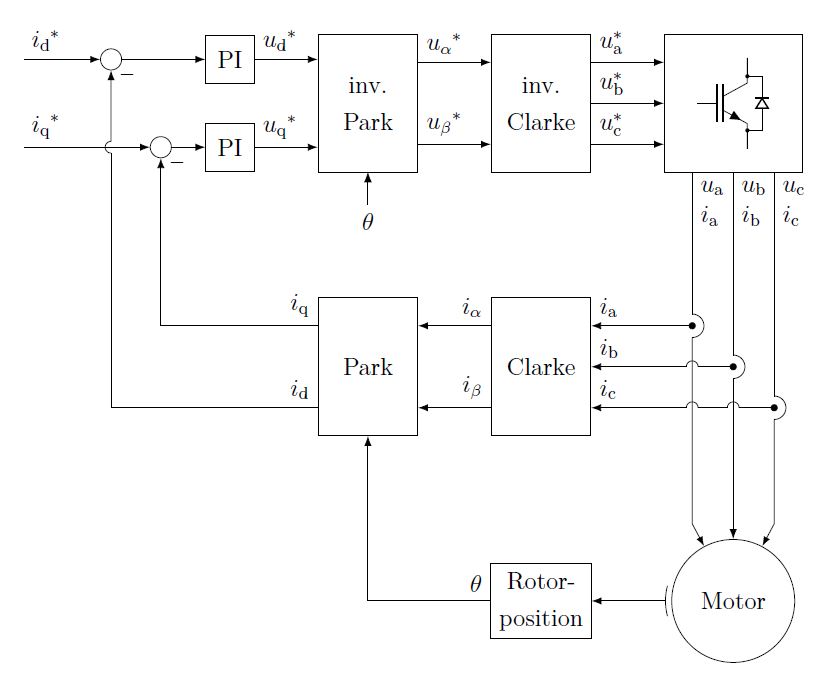
Abb. 7: Feldorientierte Regelung einer Drehfeldmaschine
Die Information der Rotorlage ist für die feldorientierte Regelung notwendig, da das Drehfeld abhängig vom Rotorwinkel gestellt werden muss. Diese Aufgabe wird üblicherweise von Lagegebern übernommen.
Aufgrund der Park-Transformation sind die Führungsgrößen i*d und i*q im stationären Betrieb Gleichgrößen. Deswegen können für die Regelung, wie auch bei der Gleichstrommaschine üblich, PI (Proportional Integral)-Regler verwendet werden. Durch die inverse Park-Transformation entstehen dann für das Drehfeld notwendige zeitvariante Größen.
Mit dem DEWETRON Power Analyzer kann die DQ-Analyse sehr einfach durchgeführt werden, um den Messwert mit dem Sollwert der Regelung zu vergleichen.
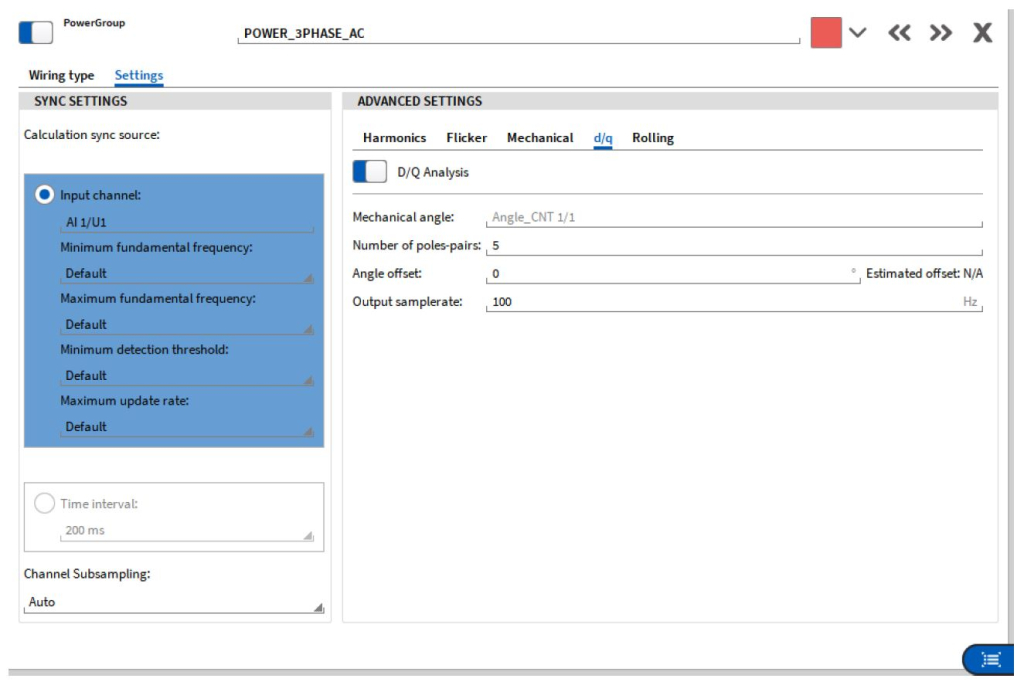
Abb. 8: DQ-Analyse in OXYGEN
DEWETRON – Ihr Spezialist für Messtechnik
DEWETRON ist ein Spezialist auf dem Gebiet der Messtechnik. Das Ziel ist, Messgeräte zu produzieren, die höchsten Qualitätsansprüchen genügen, modular und vielseitig einsetzbar sowie einfach zu bedienen sind.
Wenn Sie mehr über DEWETRON erfahren möchten, können Sie unsere DEWETRON Website besuchen. Dort finden Sie weitere Whitepapers sowie Blogposts und Videotutorials. Wir sind auch in den sozialen Medien aktiv. Werfen Sie einen Blick auf Twitter, LinkedIn oder YouTube.





